Pada dasarnya terdapat dua macam kondisi data urut, yaitu urut naik (ascending) dan urut turun (descending).berikut adalah urutan ascending dan descending jika terdapat data sebagai berikut:
Acak : 40 51 52 90 74 72 84 47 69
Ascending:40 47 51 52 69 70 72 84 90
Descending: 90 84 72 70 69 52 51 47 40
Terdapat beberapa metode pengurutan data, antara lain seleksi langsung (straight selection), gelembung (bubble sort atau exchange sort), penyisipan langsung (straight insertion), penyisipan biner (binary insertion), shell sort (diminishing increment), quick short (partition exchange sort), radix sort, serta merge sort (two way merge short).
a. Metode Seleksi Langsung
untuk memperoleh data dalam kondisi urut naik, maka prosedur yang dilakukan dalam metode ini dijelaskan sebagai berikut:
1. Langkah pertama, data terkecil harus dicari dari seluruh data dan kemudian ditempatkan pada posisi urutan pertama.
2. Langkah kedua, mencari data terkecil kedua dari seluruh data kecuali data pertama, dan kemudian ditempatkan pada posisi urutan kedua.
3. langkah ketiga, mencari data terkecil dari seluruh data kecuali data pertama dan kedua, kemudian ditempatkan pada posisi urutan ketiga.
Demikian secara terus menerus akan diulangi proses tersebut hingga semua data akan menempati posisinya secara tepat sehingga menghasilkan sekumpulan data yang urut.
Untuk lebih akan diberikan contoh penggunaan metode seleksi langsung untuk mengurutkan data-data secara urut naik dan urut turun. Data-data yang diurutkan sebagai berikut:
12 29 17 56 11 23
berikut adalah pengurutan data urut naik dengan metode seleksi langsung:
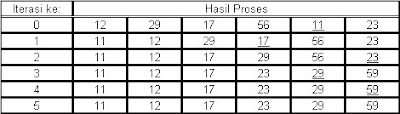
berikut adalah pengurutan data urut turun denga metode seleksi langsung:
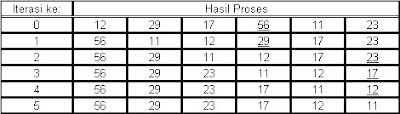
b. Metode Gelembung (Bubble Sort)
metode gelembung (bubble sort) disebut juga dengan metode exchage sort. Untuk mengurutkan data secara urut naik, jika dibandingkan dengan metode seleksi langsung maka metode gelembung memiliki perbedaan dalam menemukan elemen data terkecil dan cara pertukaran datanya.
untuk memperoleh data dalam kondisi urut naik, maka prosedur yang dilakukan dalam metode ini dijelaskan sebagai berikut:
1. Langkah pertama, pengurutan data secara urut naik dengan metoda gelembung adalah membandingkan harga data secara urut naik dengan metode gelembung adalah membandingkan harga pertama dan kedua. Jika harga pertama lebih besar maka tukarkan posisinya dengan kata kedua. Kemudian data kedua lebih besar dari data ketiga, tukarkan jika data kedua lebih besar dari data ketiga. Selanjutnya, data ketiga dibandingkan dengan data keempat, tukarkan jika data ketiga lebih besar dari data keempat. Proses ini akan diulang terus-menerus hingga semua data selesai dibandingkan.
2. Langkah kedua, harga data pertama dibandingkan dengan data kedua. Jika harga data pertama lebih besar maka ditukarkan posisinya dengan data kedua. Kemudian data kedua dibandingkan dengan data ketiga, tukarkan posisinya jika data kedua lebih besar dari data ketiga. Proses ini akan diulang terus-menerus hingga semua data selesai dibandingkan.
c. Metode Penyisipan Langsung (Straight Insertion)
Metode penyisipan langsung merupakan kebalikan dari proses yang telah dilakukan dalam metode seleksi langsung.
Berikut adalah langkah-langkah untuk pengurutan data penyisipan langsung:
1. Langkah pertama, membandingkan harga data pada urutan kedua terhadap harga data pertama. Jika data kedua lebih besar, maka data kedua ditukarkan posisinya dengan data pertama.
2. Langkah kedua, data pada urutan ketiga dibandingkan dengan data pada urutan kedua. Jika data ketiga lebih besar maka, data ketiga ditukarkan posisinya dengan data kedua. Kemudian data tersebut dibandingkan dengan harga data pertama, tukarkan pisisi kedua data jika data kedua lebih besar.
3. Langkah ketiga, data keempat dibandingkan dengan terhadap data-data urut yang telah diproses, yaitu data ketiga, kedua, dan pertama, dan begitu terus selanjutnya.
d. Metode Penyisipan Biner (Binary Insertion)
Metode biner merupakan usaha perbaikan dari dua metoda penyisipan langsung (straight insertion).
Secara garis besar, proses pengurutan data dengan metoda ini terdiri dari dua bagian utama, yaitu proses penentuan elemen-elemen data yang akan diproses dan proses penyisipan elemen data untuk mengurutkan data-data. Proses penentuan elemen data yang akan diproses adalah sama dengan cara-cara dalam dalam metoda penyisipan langsung. Berbeda dengan metode penysipan langsung dimana penentuan lokasi dan penyisipan dilakukan secara langsung, maka dalam penyisipan biner penentuan lokasi dan penyisipan dilakukan dengan metode biner.
e. Metode Quick Sort (Partition Exchange Sort)
Proses metode pengurutan ini secara garis besar adalah sebagai berikut. Bila diketahui sebuah nilai vektor K dengan N buah elemen data yang akan diurutkan secara urut naik. Pertama-tama dipilih dari salah satu elemen data sembarang pada vektor K tersebut, biasanya adalah elemen pada urutan pertama dan kita beri nama X. selanjutnya semua data elemen pada vektor K disusun dengan menempatkan elemen X pada posisi tertentu yaitu J sedemikian rupa sehingga, dengan demikian akan terdapat dua buah sub vektor, yaitu sub vektor bagian pertama yang memuat elemen-elemen data yang memiliki harga lebih dari X.
Prosedur diatas akan diulang pada subvektor pertama dan subvektor kedua, sehingga akan diperoleh empat bagian subvektor baru. Proses yang sama akan terus dilakukan secara berulang-ulang hingga semua subvektor pada akhirnya hanya tinggal mempunyai satu elemen data. Dalam kondisi demikian, semua data dalam vektor K telah menjadi urut naik.
e. Metode Quick Sort (Partition Exchange Sort)
Berikut adalah langkah-langkah dalam proses pengurutan data quick sort adalah sebagai berikut:
1. Langkah pertama, data pada ururtan pertama dibandingkan dengan data pada jarak tertentu dari data pertama tersebut, misal N/6 atau N-5, N-4, N-3, N-2, N-1. Jika data pertama lebih besar, maka posisi data saling ditukarkan. Berikutnya, data pada urutan kedua dibandingkan dengan data pada jarak yang sama sebagaimana dilakukan pada data pertama. Lakukan pertukaran data dilakuakan hingga data pada ururtan terakhir (=N) selesai diproses.
2. Langkah kedua, proses perbandingan dan pertukaran data seperti diatas diulang kembali dengan jarak yang lebih kecil.
3. langkah ketiga, keempat, kelima, dan seterusnya hingga terakhir, proses perbandingan dan pertukaran, (jika diperlukan) akan terus dilakukan dengan jarak yang semakin diperkecil. Proses akan dihentikan bila jarak untuk membandingkan antara data yang sama dengan satu. Dalam kondisi demikian ini, maka smua data dalam vektor N telah menjadi urut naik.
f. Metode Merge Sort (Two-Way Merge Sort)
Secara garis besar metode merge sort diandaikan dengan sebuah vektor K dengan cacah elemen data sebanyak N dalam kondisi tidak urut. Untuk mengurutkan semua data dalam K adalah:
1. Langakh pertama, dalam setiap elemen vektor K dianggap sebagai sebuah vektor yang masing-masing mempunyai sebuah elemen data. Dengan demikian akan terdapat N vektor dengan cacah elemen masing-masing adalah 1 buah.
2. Langkah kedua, setiap pasangan vektor yang berurutkan kita gabungkan menjadi sebuah vektor baru. Jika kita menginginkan hasil secara naik, maka pada saat menggabungkan kedua vektor sekaligus dilakukan perbandingan dan pertukaran posisi antar elemen data sedemikian rupa sehingga data yang lebih kecil akan ditempatkan pada posisi yang mendahului data lain yang lebih besar.
3. Langkah ketiga, setiap pasang vektor yang berurutan dilakukan penggabungan dan sekaligus dapat pertukaran posisi antar data sehingga akan ternetuk vektor-vektor baru.
4. Langkah keempat, memeriksa cacah masing-masing vektor baru (=UKURAN) yang digunakan dalam sub iterasi untuk melakukan proses penggabungan.
5. Langkah kelima, menginisialisasi variabel-variabel I,J, dan T yang digunakan sebagai indeks vektor yang akan digabungkan.
6. Langkah keenam hingga langkah ke delapan merupakan prosedur untuk melakukan penggabungan.
f. Metode Radix Sort
Metode radix yaitu metode pengurutan data didasarkan pada harga sesungguhnya dari suatu digit pada bilangan-bilangan yang hendak diurutkan. Dalam basis sistem bilangan desimal, maka digit-digit suatu bilangan dapat dikelompokkan menjadi 10 kelompok, yaitu kelompok “0”, ”1”, ”2”, “3”, “4”, “5”, “6”, “7”, “8”, “9”. Dengan demikian harga suatu bilangan dapat diidentifikasikan ked ala kelompok-kelompok digit tersebut.
Sumber:
Sutanta, Edhy., 2004, Algoritma Teknik Penyelesaian Permasalahan Untuk Komputasi, PT Graha Ilmu, Yogyakarta.
Tidak ada komentar:
Posting Komentar